Silakan sampaikan pada forum ini jika ada hal-hal yang kurang jelas atau sulit Anda pahami terkait materi BAB I. Terima kasih.
Ayo Diskusi
Nama : Ririn Oriska
Npm : 2013022010
izin bertanya pak,
Dalam aljabar vektor, pada bagian vektor posisi, perpindahan, dan pemisahan terdapat istilah vektor posisi . Ada berapa macamkah vektor posisi dan jelaskan?
Terimakasih
Npm : 2013022010
izin bertanya pak,
Dalam aljabar vektor, pada bagian vektor posisi, perpindahan, dan pemisahan terdapat istilah vektor posisi . Ada berapa macamkah vektor posisi dan jelaskan?
Terimakasih
Nama : Gustin Wardani
NPM : 2013022030
Izin menjawab,
Vektor posisi adalah vektor yang menggambarkan posisi di suatu titik. Suatu benda yang berada di koordinat x,y dapat dituliskan posisinya sebagai berikut.
NPM : 2013022030
Izin menjawab,
Vektor posisi adalah vektor yang menggambarkan posisi di suatu titik. Suatu benda yang berada di koordinat x,y dapat dituliskan posisinya sebagai berikut.

Untuk mengetahui jarak benda dari pusat koordinat, dapat ditentukan dari besarnya vektor posisi tersebut.


Terima Kasih
Nama : Pita Nadia
NPM : 2013022008
Izin menjawab,
Letak atau lokasi suatu titik dalam tiga dan 2 dimensi dapat dijelaskan dengan membuatnya ke koordinat kartesius. Untuk 2 dimensi (x, y) sedangkan untuk 3 dimensi (x,y,z). Vektor dari titik tersebut ke titik asal disebut vektor posisi.
- Pada 3 dimensi dapat ditulis posisinya, yaitu:
NPM : 2013022008
Izin menjawab,
Letak atau lokasi suatu titik dalam tiga dan 2 dimensi dapat dijelaskan dengan membuatnya ke koordinat kartesius. Untuk 2 dimensi (x, y) sedangkan untuk 3 dimensi (x,y,z). Vektor dari titik tersebut ke titik asal disebut vektor posisi.
- Pada 3 dimensi dapat ditulis posisinya, yaitu:
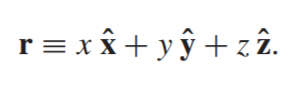
untuk mengitung jarak dari titik asal:
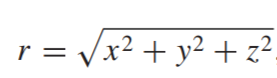
dan
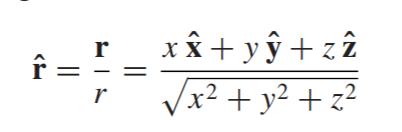
adalah vektor satuan yang menunjuk secara radial ke luar.
- Sedangkan pada 2 dimensi dapat ditulis posisinya, yaitu:
untuk mengitung jarak dari titik asal:
Terima kasih
Nama : Latia Merinda
NPM : 2013022026
Izin menjawab
Berdasarkan ruang yang ditempati maka vektor dapat dibagi menjadi dua (2) jenis yaitu vektor dimensi dua dan vektor dimensi tiga.
1. Vektor dimensi dua
Ini adalah vektor yang menempati ruang dimensi dua (R2). Vektor ini memiliki dua komponen dan digambarkan pada bidang koordinat Cartecius dengan sumbu x dan sumbu y. Adapun bentuk umum vektor dimensi dua adalah , dengan a dan b adalah scalar. Misalkan terdapat titik P (p1.p2) dan titik Q (q1.q2). Vektor PQ dapat dituliskan dalam vektor komponen menjadi PQ = (q1 – p1) i + (q2– p2)j
2. Vektor dimensi tiga
Ini adalah vektor yang menempati ruang dimensi tiga (R3). Vektor ini memiliki tiga komponen dan digambarkan pada koordinat ruang Cartesius dengan sumbu x, sumbu y, dan sumbu z. Bentuk umumnya adalah x = ai + bj + ck dengan a, b, dan c adalah scalar. Misalkan terdapat titik P (p1, p2, p3) dan titik Q (q1 + q2 + q3). Vektor PQ dapat dituliskan dalam vektor komponen menjadi PQ = (q1 – p1)i + (q2 – p2)j + (q3 – p3)k.
Terimakasih
NPM : 2013022026
Izin menjawab
Berdasarkan ruang yang ditempati maka vektor dapat dibagi menjadi dua (2) jenis yaitu vektor dimensi dua dan vektor dimensi tiga.
1. Vektor dimensi dua
Ini adalah vektor yang menempati ruang dimensi dua (R2). Vektor ini memiliki dua komponen dan digambarkan pada bidang koordinat Cartecius dengan sumbu x dan sumbu y. Adapun bentuk umum vektor dimensi dua adalah , dengan a dan b adalah scalar. Misalkan terdapat titik P (p1.p2) dan titik Q (q1.q2). Vektor PQ dapat dituliskan dalam vektor komponen menjadi PQ = (q1 – p1) i + (q2– p2)j
2. Vektor dimensi tiga
Ini adalah vektor yang menempati ruang dimensi tiga (R3). Vektor ini memiliki tiga komponen dan digambarkan pada koordinat ruang Cartesius dengan sumbu x, sumbu y, dan sumbu z. Bentuk umumnya adalah x = ai + bj + ck dengan a, b, dan c adalah scalar. Misalkan terdapat titik P (p1, p2, p3) dan titik Q (q1 + q2 + q3). Vektor PQ dapat dituliskan dalam vektor komponen menjadi PQ = (q1 – p1)i + (q2 – p2)j + (q3 – p3)k.
Terimakasih
Nama : Latia Merinda
NPM : 2013022026
Izin bertanya
Apa yang membedakan koordinat kurvilinear dengan fungsi dirac delta?
Terimakasih
NPM : 2013022026
Izin bertanya
Apa yang membedakan koordinat kurvilinear dengan fungsi dirac delta?
Terimakasih
Nama: Rosa Salsabila Latifah
NPM: 2013022050
Izin menjawab,
Koordinat kulvilinier merupakan suatu sistem koordinat yang koordinatnya berupa garis/bidang (lurus/lengkung), sedangkan fungsi dirac delta digunakan untuk merepresentasikan objek titik ideal, seperti titik titik atau muatan titik. Fungsi dirac delta ini biasanya digunakan dalam fungsi gelombang kuantum, Fungsi delta diwakili dengan simbol delta huruf kecil Yunani, ditulis sebagai fungsi: δ ( x ).
Terima kasih.
NPM: 2013022050
Izin menjawab,
Koordinat kulvilinier merupakan suatu sistem koordinat yang koordinatnya berupa garis/bidang (lurus/lengkung), sedangkan fungsi dirac delta digunakan untuk merepresentasikan objek titik ideal, seperti titik titik atau muatan titik. Fungsi dirac delta ini biasanya digunakan dalam fungsi gelombang kuantum, Fungsi delta diwakili dengan simbol delta huruf kecil Yunani, ditulis sebagai fungsi: δ ( x ).
Terima kasih.
Nama : Putri Asnaul Karimah
NPM : 2013022014
Izin bertanya,
Bagaimana hubungan yang dihasilkan antara perkalian titik dengan perkalian vektor?
Terimakasih
NPM : 2013022014
Izin bertanya,
Bagaimana hubungan yang dihasilkan antara perkalian titik dengan perkalian vektor?
Terimakasih
Nama : Pita Nadia
NPM : 2013022008
Izin menjawab,
perkalian vektor dapat dilakukan menggunakan perkalian titik (dot) atau perkalian silang (cross). Hasil dari perkalian vektor dengan menggunakan perkalian titik (dot) berupa skalar. Contoh: pada kasus u=v atau dapat ditulis u.v ,maka hasil perkalian titik u dan v adalah
Oleh sebab itu antara perkalian vektor dengan perkalian perkalian titik berhubungan erat karena perkalian vektor jika tidak menggunakan kali silang (cross) maka menggunakan perkalian titik (dot).
Terima kasih
NPM : 2013022008
Izin menjawab,
perkalian vektor dapat dilakukan menggunakan perkalian titik (dot) atau perkalian silang (cross). Hasil dari perkalian vektor dengan menggunakan perkalian titik (dot) berupa skalar. Contoh: pada kasus u=v atau dapat ditulis u.v ,maka hasil perkalian titik u dan v adalah

Oleh sebab itu antara perkalian vektor dengan perkalian perkalian titik berhubungan erat karena perkalian vektor jika tidak menggunakan kali silang (cross) maka menggunakan perkalian titik (dot).
Terima kasih
Nama : Winda Dwi Safitri
NPM : 2013022018
Izin menjawab,
NPM : 2013022018
Izin menjawab,

Terima Kasih
Nama : Pita Nadia
NPM : 2013022008
Izin bertanya,
Dalam buku Griffith (edisi ke-4), menjelaskan bahwa biasanya nilai integral garis sangat bergantung pada lintasan yang diambil dari a ke b, tetapi ada kelas khusus fungsi vektor yang penting di mana integral garis tidak bergantung pada jalur dan ditentukan seluruhnya oleh titik akhir.
Bagaimana cara membedakan integral garis tersebut masuk ke kelas khusus (ditentukan seluruhnya oleh titik akhir) atau bukan?
Terima kasih
NPM : 2013022008
Izin bertanya,
Dalam buku Griffith (edisi ke-4), menjelaskan bahwa biasanya nilai integral garis sangat bergantung pada lintasan yang diambil dari a ke b, tetapi ada kelas khusus fungsi vektor yang penting di mana integral garis tidak bergantung pada jalur dan ditentukan seluruhnya oleh titik akhir.
Bagaimana cara membedakan integral garis tersebut masuk ke kelas khusus (ditentukan seluruhnya oleh titik akhir) atau bukan?
Terima kasih
Nama : Alfia Rosa
NPM : 2013022040
Izin bertanya, bagaimana komponen vektor dan turunan vektor pada koordinat umum lengkung bekerja?
Terima kasih
NPM : 2013022040
Izin bertanya, bagaimana komponen vektor dan turunan vektor pada koordinat umum lengkung bekerja?
Terima kasih
Nama : Insani Triana
NPM : 2013022002
Izin bertanya,
Pada buku Griffith (edisi ke-4) materi direct delta function, mengapa nilai integral permukaan itu tidak bergantung pada nilai R?
Terima kasih
NPM : 2013022002
Izin bertanya,
Pada buku Griffith (edisi ke-4) materi direct delta function, mengapa nilai integral permukaan itu tidak bergantung pada nilai R?
Terima kasih
Nama : Chairani Kartini S.Harry
NPM : 2013022028
Izin bertanya,
Mengapakah koordinat lengkung sering digunakan untuk menentukan lokasi atau distribusi kuantitas fisik yang mungkin, misalnya, skalar , vektor , atau tensor?
Terima kasih
NPM : 2013022028
Izin bertanya,
Mengapakah koordinat lengkung sering digunakan untuk menentukan lokasi atau distribusi kuantitas fisik yang mungkin, misalnya, skalar , vektor , atau tensor?
Terima kasih
Nama : Mita Safira
NPM : 2013022044
Izin menjawab,
Karena ekspresi matematika yang melibatkan kuantitas ini dalam kalkulus vektor dan analisis tensor (seperti gradien , divergensi , curl , dan Laplacian ) dapat diubah dari satu sistem koordinat ke sistem koordinat lainnya, sesuai dengan aturan transformasi untuk skalar, vektor, dan tensor. Ekspresi tersebut kemudian menjadi valid untuk setiap sistem koordinat lengkung.
Terimakasih
NPM : 2013022044
Izin menjawab,
Karena ekspresi matematika yang melibatkan kuantitas ini dalam kalkulus vektor dan analisis tensor (seperti gradien , divergensi , curl , dan Laplacian ) dapat diubah dari satu sistem koordinat ke sistem koordinat lainnya, sesuai dengan aturan transformasi untuk skalar, vektor, dan tensor. Ekspresi tersebut kemudian menjadi valid untuk setiap sistem koordinat lengkung.
Terimakasih
Nama : Dian Permata Hati
NPM : 2013022036
Izin bertanya, bagaimana keadaan vektor dua dimensi?
Terimakasih
NPM : 2013022036
Izin bertanya, bagaimana keadaan vektor dua dimensi?
Terimakasih
Nama : Sihfa Zhainita
NPM : 2013022062
Izin menjawab,
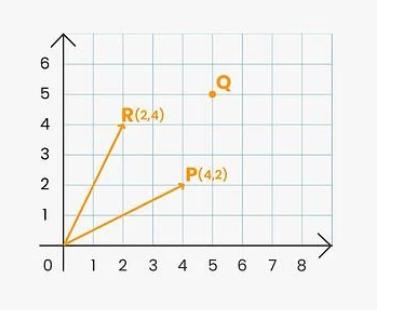
Vektor pada bidang bisa disebut juga sebagai vektor dua dimensi. Pada vektor dua dimensi, kita akan mengenal yang namanya vektor posisi. Vektor Posisi adalah vektor yang berpangkal di pusat koordinat (0,0) dan berujung di suatu titik (x,y).
Jika diperhatikan terdapat dua buah ruas garis, yaitu OP dan OR. Kita misalkan ruas garis OP sebagai vektor p dan ruas garis ORsebagai vektor R. Vektor p termasuk vektor posisi karena memiliki pangkal di pusat koordinat O (0,0) dan ujung di titik P (4,2). Sama halnya dengan vektor R yang juga merupakan vektor posisi karena berpangkal di titik O (0,0) dan ujung di titik R (2,4).
Terima kasih
NPM : 2013022062
Izin menjawab,
Vektor pada bidang bisa disebut juga sebagai vektor dua dimensi. Pada vektor dua dimensi, kita akan mengenal yang namanya vektor posisi. Vektor Posisi adalah vektor yang berpangkal di pusat koordinat (0,0) dan berujung di suatu titik (x,y).
Jika diperhatikan terdapat dua buah ruas garis, yaitu OP dan OR. Kita misalkan ruas garis OP sebagai vektor p dan ruas garis ORsebagai vektor R. Vektor p termasuk vektor posisi karena memiliki pangkal di pusat koordinat O (0,0) dan ujung di titik P (4,2). Sama halnya dengan vektor R yang juga merupakan vektor posisi karena berpangkal di titik O (0,0) dan ujung di titik R (2,4).

Terima kasih
Nama : Sihfa Zhainita
NPM : 2013022062
Izin bertanya,
Bagaimana cara menentukan suatu titik berada pada kuadran koordinat kartesius?
Terima kasih
NPM : 2013022062
Izin bertanya,
Bagaimana cara menentukan suatu titik berada pada kuadran koordinat kartesius?
Terima kasih
Nama : Dian Permata Hati
NPM : 2013022036
Izin menjawab,
Kuadran koordinat Cartesius ada 4. Pada kuadran I nilai x positif y positif, pada kuadran II nilai x negatif y positif, pada kuadran III nilai x negatif y negatif, dan pada kuadran IV nilai x positif y negatif.
Ringkasnya:
- KI letak titik (a, b)
- KII letak titik (-a, b)
- KIII letak titik (-a, -b)
- KIV letak titik (a, -b)
Terimakasih
NPM : 2013022036
Izin menjawab,
Kuadran koordinat Cartesius ada 4. Pada kuadran I nilai x positif y positif, pada kuadran II nilai x negatif y positif, pada kuadran III nilai x negatif y negatif, dan pada kuadran IV nilai x positif y negatif.
Ringkasnya:
- KI letak titik (a, b)
- KII letak titik (-a, b)
- KIII letak titik (-a, -b)
- KIV letak titik (a, -b)
Terimakasih
Nama : Neo Safitri
NPM : 2013022006
Izin bertanya,
Pada aljabar vektor terdapat bagian vektor perpindahan, bagaimana komponen dan rumus perpindahan pada vektor tersebut?
Terimakasih.
NPM : 2013022006
Izin bertanya,
Pada aljabar vektor terdapat bagian vektor perpindahan, bagaimana komponen dan rumus perpindahan pada vektor tersebut?
Terimakasih.
Nama : Sholea Mutiara
Npm : 2013022048
Izin bertanya,
Sebutkan dan jelaskan fungsi dari delta dirac, yang paling umum dan sering digunakan?
Terima kasih.
Npm : 2013022048
Izin bertanya,
Sebutkan dan jelaskan fungsi dari delta dirac, yang paling umum dan sering digunakan?
Terima kasih.
