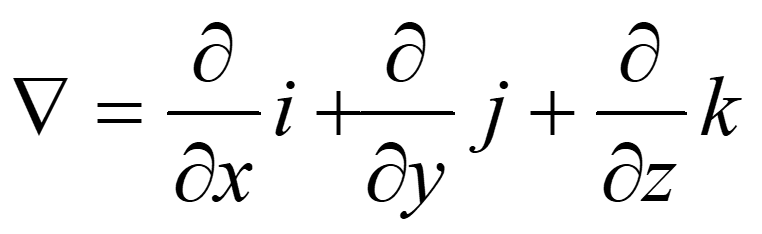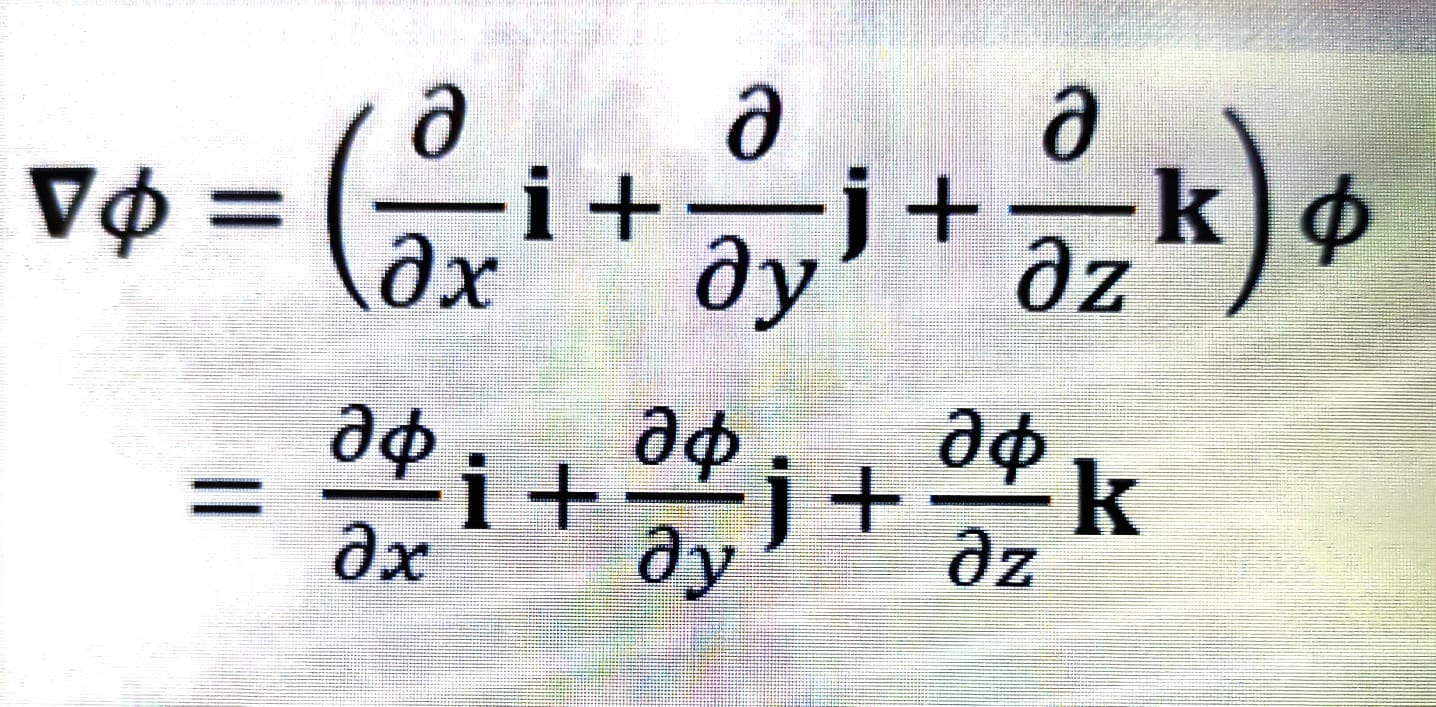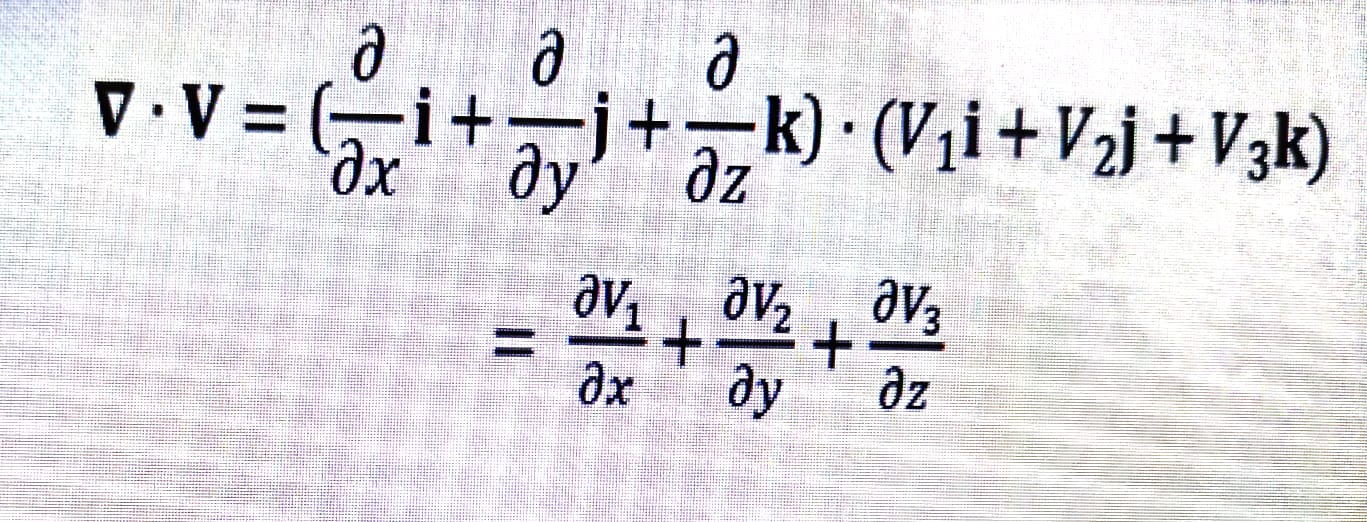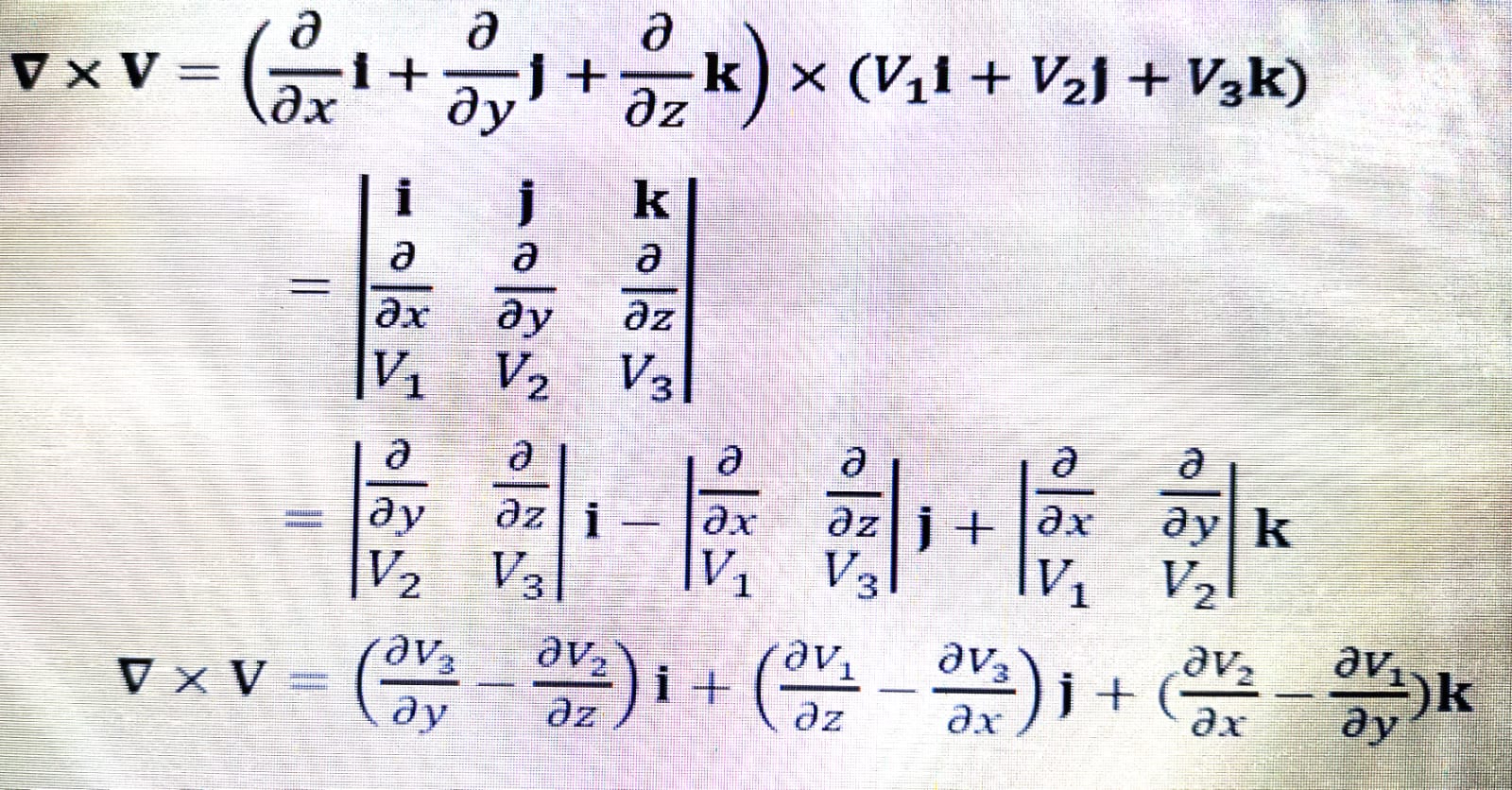Silakan Anda pahami Peranti Matematis (Mathematical Tools) berupa ANALISIS VEKTOR dari buku Griffith (Edisi ke-4). Anda dapat menggunakan sumber lain juga untuk menguatkan pemahaman Anda terkait ANALISIS VEKTOR. Adapun yang perlu Anda pelajari:
- Aljabar Vektor (Penjumlahan & Pengurangan Vektor, Perkalian Vektor, Triple Products)
- Kalkulus Diferensial (Gradien, Divergensi, Curl)
- Kalkulus Integral (Integral lintasan, permukaan, dan volume; Teorema Gradiensi, Teorema Divergensi, Teorema Curl)
- Koordinat Melengkung (Permukaan Bola dan Silinder)
- Fungsi Delta Dirac