Untuk menguatkan pemahaman Anda terkait sistem koordinat. Silakan Anda menonton penjelasan sistem koordinat Cartesian dan Sistem Koordinat Melengkung (Spherical & Cylindrical Coordinate System).
Ayo Diskusi: Sistem Koordinat Bola
Nama : Ananda Resya Putri
Npm : 2013022011
Izin bertanya
Npm : 2013022011
Izin bertanya
Dijelaskan dalam video bahwa Sistem koordinat lengkung mungkin lebih mudah digunakan daripada sistem koordinat Cartesian untuk beberapa aplikasi. Mengapa demikian?
Terimakasih
Terimakasih
Nama: Triana Sofia
NPM: 2013022055
Izin mencoba menjawab pertanyaan dari saudari Ananda Resya Putri.
Sistem koordinat lengkung mungkin lebih mudah digunakan daripada sistem koordinat Cartesian untuk beberapa aplikasi. Gerak partikel di bawah pengaruh gaya pusat biasanya lebih mudah diselesaikan dalam koordinat bola daripada di koordinat Cartesian. Ini benar untuk banyak masalah fisik dengan simetri bola yang didefinisikan dalam R3. Persamaan dengan kondisi batas yang mengikuti permukaan koordinat untuk sistem koordinat lengkung tertentu mungkin lebih mudah diselesaikan dalam sistem itu. Sementara orang mungkin menggambarkan gerakan partikel dalam kotak persegi panjang menggunakan koordinat Cartesian, gerakan dalam bola lebih mudah dengan koordinat bola.
Sekian jawaban dari saya. Mohon maaf apabila terdapat kesalahan dalam penyampaian.
Terima kasih.
NPM: 2013022055
Izin mencoba menjawab pertanyaan dari saudari Ananda Resya Putri.
Sistem koordinat lengkung mungkin lebih mudah digunakan daripada sistem koordinat Cartesian untuk beberapa aplikasi. Gerak partikel di bawah pengaruh gaya pusat biasanya lebih mudah diselesaikan dalam koordinat bola daripada di koordinat Cartesian. Ini benar untuk banyak masalah fisik dengan simetri bola yang didefinisikan dalam R3. Persamaan dengan kondisi batas yang mengikuti permukaan koordinat untuk sistem koordinat lengkung tertentu mungkin lebih mudah diselesaikan dalam sistem itu. Sementara orang mungkin menggambarkan gerakan partikel dalam kotak persegi panjang menggunakan koordinat Cartesian, gerakan dalam bola lebih mudah dengan koordinat bola.
Sekian jawaban dari saya. Mohon maaf apabila terdapat kesalahan dalam penyampaian.
Terima kasih.
In reply to Ananda Resya Putri 2013022011
Re: Ayo Diskusi: Sistem Koordinat Bola
Nama: Sri Wahyu Lestari
Npm: 2013022031
Izin menjawab pertanyaan dari Nanda
Karena Gerak partikel di bawah pengaruh gaya pusat biasanya lebih mudah diselesaikan dalam koordinat bola daripada di koordinat Cartesian.
Sementara seseorang mungkin menggambarkan gerakan partikel dalam kotak persegi panjang menggunakan koordinat Cartesian, gerakan dalam bola lebih mudah dengan koordinat bola.
Terimakasih
Npm: 2013022031
Izin menjawab pertanyaan dari Nanda
Karena Gerak partikel di bawah pengaruh gaya pusat biasanya lebih mudah diselesaikan dalam koordinat bola daripada di koordinat Cartesian.
Sementara seseorang mungkin menggambarkan gerakan partikel dalam kotak persegi panjang menggunakan koordinat Cartesian, gerakan dalam bola lebih mudah dengan koordinat bola.
Terimakasih
In reply to Ananda Resya Putri 2013022011
Re: Ayo Diskusi: Sistem Koordinat Bola
Nama: Winda Lestari
NPM: 2013022045
Izin menjawab pertanyaan dari saudari Ananda,
Koordinat lengkung mungkin lebih mudah digunakan daripada sistem koordinat Cartesian sebab sebagai contoh, untuk masalah fisik dengan simetri bola yang didefinisikan dalam R³ akan lebih mudah diselesaikan dengan koordinat lengkung. Hal ini dikarenakan persamaan dengan kondisi batas yang mengikuti permukaan koordinat untuk sistem koordinat lengkung tertentu mungkin lebih mudah diselesaikan dalam sistem itu.
Mohon maaf apabila ada kesalahan, terima kasih
NPM: 2013022045
Izin menjawab pertanyaan dari saudari Ananda,
Koordinat lengkung mungkin lebih mudah digunakan daripada sistem koordinat Cartesian sebab sebagai contoh, untuk masalah fisik dengan simetri bola yang didefinisikan dalam R³ akan lebih mudah diselesaikan dengan koordinat lengkung. Hal ini dikarenakan persamaan dengan kondisi batas yang mengikuti permukaan koordinat untuk sistem koordinat lengkung tertentu mungkin lebih mudah diselesaikan dalam sistem itu.
Mohon maaf apabila ada kesalahan, terima kasih
In reply to Ananda Resya Putri 2013022011
Re: Ayo Diskusi: Sistem Koordinat Bola
Nama : Dwi Anggi Oktaviani
NPM : 2013022025
Izin menjawab pertanyaan dari saudari Ananda Resya Putri,
Gerakan partikel di bawah pengaruh gaya pusat biasanya lebih mudah diselesaikan dalam koordinat bola daripada dalam koordinat Cartesian; ini benar untuk banyak masalah fisik dengan simetri bola yang didefinisikan dalam R 3 . Persamaan dengan kondisi batasyang mengikuti permukaan koordinat untuk sistem koordinat lengkung tertentu mungkin lebih mudah diselesaikan dalam sistem itu. Sementara orang mungkin menggambarkan gerakan partikel dalam kotak persegi panjang menggunakan koordinat Cartesian, gerakan dalam bola lebih mudah dengan koordinat bola. Koordinat bola adalah sistem koordinat lengkung yang paling umum dan digunakan dalam ilmu bumi , kartografi , mekanika kuantum , relativitas , dan teknik .
Terimakasih.
NPM : 2013022025
Izin menjawab pertanyaan dari saudari Ananda Resya Putri,
Gerakan partikel di bawah pengaruh gaya pusat biasanya lebih mudah diselesaikan dalam koordinat bola daripada dalam koordinat Cartesian; ini benar untuk banyak masalah fisik dengan simetri bola yang didefinisikan dalam R 3 . Persamaan dengan kondisi batasyang mengikuti permukaan koordinat untuk sistem koordinat lengkung tertentu mungkin lebih mudah diselesaikan dalam sistem itu. Sementara orang mungkin menggambarkan gerakan partikel dalam kotak persegi panjang menggunakan koordinat Cartesian, gerakan dalam bola lebih mudah dengan koordinat bola. Koordinat bola adalah sistem koordinat lengkung yang paling umum dan digunakan dalam ilmu bumi , kartografi , mekanika kuantum , relativitas , dan teknik .
Terimakasih.
In reply to Ananda Resya Putri 2013022011
Re: Ayo Diskusi: Sistem Koordinat Bola
Nama: Cahya Nur Candini
NPM: 2013022013
Izin menjawab pertanyaan saudari ananda mengenai mengapa Sistem koordinat lengkung mungkin lebih mudah digunakan daripada sistem koordinat Cartesian.
Dalam geometri , koordinat lengkung adalah sistem koordinat untuk ruang Euclidean di mana garis koordinat dapat melengkung. Koordinat ini dapat diturunkan dari himpunan koordinat Cartesius dengan menggunakan transformasi yang dapat dibalik secara lokal (peta satu-ke-satu) di setiap titik. Ini berarti bahwa seseorang dapat mengubah titik yang diberikan dalam sistem koordinat Cartesian ke koordinat lengkung dan kembali. Nama koordinat lengkung , diciptakan oleh ahli matematika Prancis Lamé , berasal dari fakta bahwa permukaan koordinat sistem lengkung melengkung.
Koordinat lengkung sering digunakan untuk menentukan lokasi atau distribusi besaran fisika yang mungkin, misalnya, skalar , vektor , atau tensor . Ekspresi matematika yang melibatkan kuantitas ini dalam kalkulus vektor dan analisis tensor (seperti gradien , divergensi , curl , dan Laplacian ) dapat diubah dari satu sistem koordinat ke sistem koordinat lainnya, sesuai dengan aturan transformasi untuk skalar, vektor, dan tensor. Ekspresi tersebut kemudian menjadi valid untuk setiap sistem koordinat lengkung.
Sistem koordinat lengkung mungkin lebih sederhana untuk digunakan daripada sistem koordinat Cartesian untuk beberapa aplikasi. Gerakan partikel di bawah pengaruh gaya pusat biasanya lebih mudah diselesaikan dalam koordinat bola daripada dalam koordinat Cartesian; ini benar untuk banyak masalah fisik dengan simetri bola yang didefinisikan dalam R 3 . Persamaan dengan kondisi batasyang mengikuti permukaan koordinat untuk sistem koordinat lengkung tertentu mungkin lebih mudah diselesaikan dalam sistem itu. Sementara orang mungkin menggambarkan gerakan partikel dalam kotak persegi panjang menggunakan koordinat Cartesian, gerakan dalam bola lebih mudah dengan koordinat bola. Koordinat bola adalah sistem koordinat lengkung yang paling umum dan digunakan dalam ilmu bumi , kartografi , mekanika kuantum , relativitas , dan teknik
Terimakasih
NPM: 2013022013
Izin menjawab pertanyaan saudari ananda mengenai mengapa Sistem koordinat lengkung mungkin lebih mudah digunakan daripada sistem koordinat Cartesian.
Dalam geometri , koordinat lengkung adalah sistem koordinat untuk ruang Euclidean di mana garis koordinat dapat melengkung. Koordinat ini dapat diturunkan dari himpunan koordinat Cartesius dengan menggunakan transformasi yang dapat dibalik secara lokal (peta satu-ke-satu) di setiap titik. Ini berarti bahwa seseorang dapat mengubah titik yang diberikan dalam sistem koordinat Cartesian ke koordinat lengkung dan kembali. Nama koordinat lengkung , diciptakan oleh ahli matematika Prancis Lamé , berasal dari fakta bahwa permukaan koordinat sistem lengkung melengkung.
Koordinat lengkung sering digunakan untuk menentukan lokasi atau distribusi besaran fisika yang mungkin, misalnya, skalar , vektor , atau tensor . Ekspresi matematika yang melibatkan kuantitas ini dalam kalkulus vektor dan analisis tensor (seperti gradien , divergensi , curl , dan Laplacian ) dapat diubah dari satu sistem koordinat ke sistem koordinat lainnya, sesuai dengan aturan transformasi untuk skalar, vektor, dan tensor. Ekspresi tersebut kemudian menjadi valid untuk setiap sistem koordinat lengkung.
Sistem koordinat lengkung mungkin lebih sederhana untuk digunakan daripada sistem koordinat Cartesian untuk beberapa aplikasi. Gerakan partikel di bawah pengaruh gaya pusat biasanya lebih mudah diselesaikan dalam koordinat bola daripada dalam koordinat Cartesian; ini benar untuk banyak masalah fisik dengan simetri bola yang didefinisikan dalam R 3 . Persamaan dengan kondisi batasyang mengikuti permukaan koordinat untuk sistem koordinat lengkung tertentu mungkin lebih mudah diselesaikan dalam sistem itu. Sementara orang mungkin menggambarkan gerakan partikel dalam kotak persegi panjang menggunakan koordinat Cartesian, gerakan dalam bola lebih mudah dengan koordinat bola. Koordinat bola adalah sistem koordinat lengkung yang paling umum dan digunakan dalam ilmu bumi , kartografi , mekanika kuantum , relativitas , dan teknik
Terimakasih
In reply to Ananda Resya Putri 2013022011
Re: Ayo Diskusi: Sistem Koordinat Bola
Nama: Yunita Safitri
NPM: 2013022039
Izin menjawab pertanyaan dari saudari Ananda,
Sistem koordinat lengkung mungkin lebih mudah digunakan daripada sistem koordinat Cartesian untuk beberapa aplikasi. Gerak partikel di bawah pengaruh gaya pusat biasanya lebih mudah diselesaikan dalam koordinat bola daripada di koordinat Cartesian. Ini benar untuk banyak masalah fisik dengan simetri bola yang didefinisikan dalam R3. Persamaan dengan kondisi batas yang mengikuti permukaan koordinat untuk sistem koordinat lengkung tertentu mungkin lebih mudah diselesaikan dalam sistem itu. Sementara orang mungkin menggambarkan gerakan partikel dalam kotak persegi panjang menggunakan koordinat Cartesian, gerakan dalam bola lebih mudah dengan koordinat bola.
Sekian, Terima kasih.
NPM: 2013022039
Izin menjawab pertanyaan dari saudari Ananda,
Sistem koordinat lengkung mungkin lebih mudah digunakan daripada sistem koordinat Cartesian untuk beberapa aplikasi. Gerak partikel di bawah pengaruh gaya pusat biasanya lebih mudah diselesaikan dalam koordinat bola daripada di koordinat Cartesian. Ini benar untuk banyak masalah fisik dengan simetri bola yang didefinisikan dalam R3. Persamaan dengan kondisi batas yang mengikuti permukaan koordinat untuk sistem koordinat lengkung tertentu mungkin lebih mudah diselesaikan dalam sistem itu. Sementara orang mungkin menggambarkan gerakan partikel dalam kotak persegi panjang menggunakan koordinat Cartesian, gerakan dalam bola lebih mudah dengan koordinat bola.
Sekian, Terima kasih.
In reply to Ananda Resya Putri 2013022011
Re: Ayo Diskusi: Sistem Koordinat Bola
by Putri Permata Sari -
Nama : Putri Permata Sari
Npm : 2013022029
Izin menjawab
Sistem koordinat lengkung mungkin lebih mudah digunakan daripada sistem koordinat Cartesian untuk beberapa aplikasi. Gerak partikel di bawah pengaruh gaya pusat biasanya lebih mudah diselesaikan dalam koordinat bola daripada di koordinat Cartesian; ini benar untuk banyak masalah fisik dengan simetri bola yang didefinisikan dalam R³ . Persamaan dengan kondisi batasyang mengikuti permukaan koordinat untuk sistem koordinat lengkung tertentu mungkin lebih mudah diselesaikan dalam sistem itu. Sementara orang mungkin menggambarkan gerakan partikel dalam kotak persegi panjang menggunakan koordinat Cartesian, gerakan dalam bola lebih mudah dengan koordinat bola. Koordinat bola adalah sistem koordinat lengkung yang paling umum dan digunakan dalam ilmu bumi , kartografi , mekanika kuantum , relativitas , dan teknik .
Terima kasih
Npm : 2013022029
Izin menjawab
Sistem koordinat lengkung mungkin lebih mudah digunakan daripada sistem koordinat Cartesian untuk beberapa aplikasi. Gerak partikel di bawah pengaruh gaya pusat biasanya lebih mudah diselesaikan dalam koordinat bola daripada di koordinat Cartesian; ini benar untuk banyak masalah fisik dengan simetri bola yang didefinisikan dalam R³ . Persamaan dengan kondisi batasyang mengikuti permukaan koordinat untuk sistem koordinat lengkung tertentu mungkin lebih mudah diselesaikan dalam sistem itu. Sementara orang mungkin menggambarkan gerakan partikel dalam kotak persegi panjang menggunakan koordinat Cartesian, gerakan dalam bola lebih mudah dengan koordinat bola. Koordinat bola adalah sistem koordinat lengkung yang paling umum dan digunakan dalam ilmu bumi , kartografi , mekanika kuantum , relativitas , dan teknik .
Terima kasih
In reply to Ananda Resya Putri 2013022011
Re: Ayo Diskusi: Sistem Koordinat Bola
Nama : Indah Viona Fittri
NPM : 2013022057
Izin menjawab pertanyaan saudari Ananda, karena Sistem koordinat lengkung mungkin lebih sederhana untuk digunakan daripada sistem koordinat Cartesian untuk beberapa aplikasi. Gerakan partikel di bawah pengaruh gaya pusat biasanya lebih mudah diselesaikan dalam koordinat bola daripada dalam koordinat Cartesian; ini benar untuk banyak masalah fisik dengan simetri bola yang didefinisikan dalam R 3 . Persamaan dengan kondisi batasyang mengikuti permukaan koordinat untuk sistem koordinat lengkung tertentu mungkin lebih mudah diselesaikan dalam sistem itu. Sementara orang mungkin menggambarkan gerakan partikel dalam kotak persegi panjang menggunakan koordinat Cartesian, gerakan dalam bola lebih mudah dengan koordinat bola. Koordinat bola adalah sistem koordinat lengkung yang paling umum dan digunakan dalam ilmu bumi , kartografi , mekanika kuantum , relativitas , dan teknik
NPM : 2013022057
Izin menjawab pertanyaan saudari Ananda, karena Sistem koordinat lengkung mungkin lebih sederhana untuk digunakan daripada sistem koordinat Cartesian untuk beberapa aplikasi. Gerakan partikel di bawah pengaruh gaya pusat biasanya lebih mudah diselesaikan dalam koordinat bola daripada dalam koordinat Cartesian; ini benar untuk banyak masalah fisik dengan simetri bola yang didefinisikan dalam R 3 . Persamaan dengan kondisi batasyang mengikuti permukaan koordinat untuk sistem koordinat lengkung tertentu mungkin lebih mudah diselesaikan dalam sistem itu. Sementara orang mungkin menggambarkan gerakan partikel dalam kotak persegi panjang menggunakan koordinat Cartesian, gerakan dalam bola lebih mudah dengan koordinat bola. Koordinat bola adalah sistem koordinat lengkung yang paling umum dan digunakan dalam ilmu bumi , kartografi , mekanika kuantum , relativitas , dan teknik
Nama: Sri Wahyu Lestari
Npm: 2013022031
Izin bertanya
Apa saja contoh sistem koordinat lengkung yang terkenal dalam ruang Euclidean tiga dimensi?
Terimakasih
Npm: 2013022031
Izin bertanya
Apa saja contoh sistem koordinat lengkung yang terkenal dalam ruang Euclidean tiga dimensi?
Terimakasih
In reply to Sri Wahyu Lestari 2013022031
Re: Ayo Diskusi: Sistem Koordinat Bola
Nama : Lu'lu' Syarqia
NPM : 2013022051
Izin menjawab pertanyaan dari Sri.
Contoh sistem koordinat lengkung yang terkenal dalam ruang Euclidean tiga dimensi ( R^3 ) adalah koordinat silinder dan bola . Permukaan koordinat Cartesian dalam ruang ini adalah bidang koordinat ; misalnya z = 0 mendefinisikan bidang x - y . Dalam ruang yang sama, permukaan koordinat r = 1 dalam koordinat bola adalah permukaan bola satuan , yang melengkung. Formalisme koordinat lengkung memberikan gambaran umum dan terpadu dari sistem koordinat standar.
Terimakasih
NPM : 2013022051
Izin menjawab pertanyaan dari Sri.
Contoh sistem koordinat lengkung yang terkenal dalam ruang Euclidean tiga dimensi ( R^3 ) adalah koordinat silinder dan bola . Permukaan koordinat Cartesian dalam ruang ini adalah bidang koordinat ; misalnya z = 0 mendefinisikan bidang x - y . Dalam ruang yang sama, permukaan koordinat r = 1 dalam koordinat bola adalah permukaan bola satuan , yang melengkung. Formalisme koordinat lengkung memberikan gambaran umum dan terpadu dari sistem koordinat standar.
Terimakasih
In reply to Sri Wahyu Lestari 2013022031
Re: Ayo Diskusi: Sistem Koordinat Bola
Nama: Lathifah Rhihadhatul Ainii
NPM: 2013022047
Izin menjawab pertanyaan dari saudari Sri Wahyu Lestari
Koordinat lengkung adalah sistem koordinat untuk ruang Euclidean di mana garis koordinat dapat melengkung. Contoh sistem koordinat lengkung yang terkenal dalam ruang Euclidean tiga dimensi ( R3 ) adalah koordinat silinder dan bola . Permukaan koordinat Cartesian dalam ruang ini adalah bidang koordinat ; misalnya z = 0 mendefinisikan bidang x - y . Dalam ruang yang sama, permukaan koordinat r = 1 dalam koordinat bola adalah permukaan bola satuan , yang melengkung. Formalisme koordinat lengkung memberikan gambaran umum dan terpadu dari sistem koordinat standar. Koordinat lengkung sering digunakan untuk menentukan lokasi atau distribusi besaran fisika yang mungkin, misalnya, skalar , vektor , atau tensor.
Terima kasih
NPM: 2013022047
Izin menjawab pertanyaan dari saudari Sri Wahyu Lestari
Koordinat lengkung adalah sistem koordinat untuk ruang Euclidean di mana garis koordinat dapat melengkung. Contoh sistem koordinat lengkung yang terkenal dalam ruang Euclidean tiga dimensi ( R3 ) adalah koordinat silinder dan bola . Permukaan koordinat Cartesian dalam ruang ini adalah bidang koordinat ; misalnya z = 0 mendefinisikan bidang x - y . Dalam ruang yang sama, permukaan koordinat r = 1 dalam koordinat bola adalah permukaan bola satuan , yang melengkung. Formalisme koordinat lengkung memberikan gambaran umum dan terpadu dari sistem koordinat standar. Koordinat lengkung sering digunakan untuk menentukan lokasi atau distribusi besaran fisika yang mungkin, misalnya, skalar , vektor , atau tensor.
Terima kasih
In reply to Lathifah Rhihadhatul Ainii 2013022047
Re: Ayo Diskusi: Sistem Koordinat Bola
Nama : Intan Nur Ajizah
Npm : 2013022037
Izin menambahkan jawaban dari saudari Lathifah
Sistem koordinat lengkung mungkin lebih sederhana untuk digunakan daripada sistem koordinat Cartesian untuk beberapa aplikasi. Gerakan partikel di bawah pengaruh gaya pusat biasanya lebih mudah diselesaikan dalam koordinat bola daripada dalam koordinat Cartesian; ini benar untuk banyak masalah fisik dengan simetri bola yang didefinisikan dalam R 3 . Persamaan dengan kondisi batasyang mengikuti permukaan koordinat untuk sistem koordinat lengkung tertentu mungkin lebih mudah diselesaikan dalam sistem itu. Sementara orang mungkin menggambarkan gerakan partikel dalam kotak persegi panjang menggunakan koordinat Cartesian, gerakan dalam bola lebih mudah dengan koordinat bola. Koordinat bola adalah sistem koordinat lengkung yang paling umum dan digunakan dalam ilmu bumi , kartografi , mekanika kuantum , relativitas , dan teknik .
Terimakasih
Npm : 2013022037
Izin menambahkan jawaban dari saudari Lathifah
Sistem koordinat lengkung mungkin lebih sederhana untuk digunakan daripada sistem koordinat Cartesian untuk beberapa aplikasi. Gerakan partikel di bawah pengaruh gaya pusat biasanya lebih mudah diselesaikan dalam koordinat bola daripada dalam koordinat Cartesian; ini benar untuk banyak masalah fisik dengan simetri bola yang didefinisikan dalam R 3 . Persamaan dengan kondisi batasyang mengikuti permukaan koordinat untuk sistem koordinat lengkung tertentu mungkin lebih mudah diselesaikan dalam sistem itu. Sementara orang mungkin menggambarkan gerakan partikel dalam kotak persegi panjang menggunakan koordinat Cartesian, gerakan dalam bola lebih mudah dengan koordinat bola. Koordinat bola adalah sistem koordinat lengkung yang paling umum dan digunakan dalam ilmu bumi , kartografi , mekanika kuantum , relativitas , dan teknik .
Terimakasih
In reply to Sri Wahyu Lestari 2013022031
Re: Ayo Diskusi: Sistem Koordinat Bola
Nama: Erna Wahyu Septianna
NPM: 2013022019
Izin menjawab pertanyaan dari saudari Sri
Contoh sistem koordinat lengkung yang terkenal dalam ruang Euclidean tiga dimensi ( R 3 ) adalah koordinat silinder dan bola . Permukaan koordinat Cartesian dalam ruang ini adalah bidang koordinat ; misalnya z = 0 mendefinisikan bidang x - y . Dalam ruang yang sama, permukaan koordinat r = 1 dalam koordinat bola adalah permukaan bola satuan , yang melengkung. Formalisme koordinat lengkung memberikan gambaran umum dan terpadu dari sistem koordinat standar.
Koordinat lengkung sering digunakan untuk menentukan lokasi atau distribusi besaran fisika yang mungkin, misalnya, skalar , vektor , atau tensor . Ekspresi matematika yang melibatkan kuantitas ini dalam kalkulus vektor dan analisis tensor (seperti gradien , divergensi , curl , dan Laplacian ) dapat diubah dari satu sistem koordinat ke sistem koordinat lainnya, sesuai dengan aturan transformasi untuk skalar, vektor, dan tensor. Ekspresi tersebut kemudian menjadi valid untuk setiap sistem koordinat lengkung.
Mohon maaf apabila terdapat kesalahan dalam menjawab,
Terimakasih
NPM: 2013022019
Izin menjawab pertanyaan dari saudari Sri
Contoh sistem koordinat lengkung yang terkenal dalam ruang Euclidean tiga dimensi ( R 3 ) adalah koordinat silinder dan bola . Permukaan koordinat Cartesian dalam ruang ini adalah bidang koordinat ; misalnya z = 0 mendefinisikan bidang x - y . Dalam ruang yang sama, permukaan koordinat r = 1 dalam koordinat bola adalah permukaan bola satuan , yang melengkung. Formalisme koordinat lengkung memberikan gambaran umum dan terpadu dari sistem koordinat standar.
Koordinat lengkung sering digunakan untuk menentukan lokasi atau distribusi besaran fisika yang mungkin, misalnya, skalar , vektor , atau tensor . Ekspresi matematika yang melibatkan kuantitas ini dalam kalkulus vektor dan analisis tensor (seperti gradien , divergensi , curl , dan Laplacian ) dapat diubah dari satu sistem koordinat ke sistem koordinat lainnya, sesuai dengan aturan transformasi untuk skalar, vektor, dan tensor. Ekspresi tersebut kemudian menjadi valid untuk setiap sistem koordinat lengkung.
Mohon maaf apabila terdapat kesalahan dalam menjawab,
Terimakasih
In reply to Sri Wahyu Lestari 2013022031
Re: Ayo Diskusi: Sistem Koordinat Bola
Nama : Nida Nafilah
NPM : 2013022059
Izin menjawab pertanyaan dari saudari Sri Wahyu Lestari,
Koordinat lengkung adalah sistem koordinat untuk ruang. Koordinat ini dapat diturunkan dari himpunan koordinat Cartesius dengan menggunakan transformasi yang dapat dibalik secara lokal (peta satu-ke-satu) di setiap titik.
Contoh sistem koordinat lengkung yang terkenal dalam ruang Euclidean tiga dimensi ( R 3 ) adalah koordinat silinder dan bola .
> Permukaan koordinat Cartesian dalam ruang ini adalah bidang koordinat ; misalnya z = 0 mendefinisikan bidang x - y .
> Dalam ruang yang sama, permukaan koordinat r = 1 dalam koordinat bola adalah permukaan bola satuan , yang melengkung. Formalisme koordinat lengkung memberikan gambaran umum dan terpadu dari sistem koordinat standar.
Terimakasih
NPM : 2013022059
Izin menjawab pertanyaan dari saudari Sri Wahyu Lestari,
Koordinat lengkung adalah sistem koordinat untuk ruang. Koordinat ini dapat diturunkan dari himpunan koordinat Cartesius dengan menggunakan transformasi yang dapat dibalik secara lokal (peta satu-ke-satu) di setiap titik.
Contoh sistem koordinat lengkung yang terkenal dalam ruang Euclidean tiga dimensi ( R 3 ) adalah koordinat silinder dan bola .
> Permukaan koordinat Cartesian dalam ruang ini adalah bidang koordinat ; misalnya z = 0 mendefinisikan bidang x - y .
> Dalam ruang yang sama, permukaan koordinat r = 1 dalam koordinat bola adalah permukaan bola satuan , yang melengkung. Formalisme koordinat lengkung memberikan gambaran umum dan terpadu dari sistem koordinat standar.
Terimakasih
In reply to Sri Wahyu Lestari 2013022031
Re: Ayo Diskusi: Sistem Koordinat Bola
Nama: Winda Lestari
NPM: 2013022045
Izin menjawab pertanyaan dari saudari Sri,
Contoh sistem koordinat lengkung yang terkenal dalam ruang Euclidean tiga dimensi adalah koordinat silinder dan bola. Permukaan koordinat Cartesian dalam ruang ini adalah bidang koordinat. Dalam ruang yang sama, permukaan koordinat r = 1 dalam koordinat bola adalah permukaan bola satuan yang melengkung.
Mohon maaf apabila ada kesalahan, terima kasih
NPM: 2013022045
Izin menjawab pertanyaan dari saudari Sri,
Contoh sistem koordinat lengkung yang terkenal dalam ruang Euclidean tiga dimensi adalah koordinat silinder dan bola. Permukaan koordinat Cartesian dalam ruang ini adalah bidang koordinat. Dalam ruang yang sama, permukaan koordinat r = 1 dalam koordinat bola adalah permukaan bola satuan yang melengkung.
Mohon maaf apabila ada kesalahan, terima kasih
In reply to Sri Wahyu Lestari 2013022031
Re: Ayo Diskusi: Sistem Koordinat Bola
Nama: Cahya Nur Candini
NPM: 2013022013
Izin menjawab pertanyaan saudari Sri mengenai contoh sistem koordinat lengkung yang terkenal dalam ruang Euclidean tiga dimensi?
Contoh sistem koordinat lengkung yang terkenal dalam ruang Euclidean tiga dimensi ( R 3 ) adalah koordinat silinder dan bola . Permukaan koordinat Cartesian dalam ruang ini adalah bidang koordinat ; misalnya z = 0 mendefinisikan bidang x - y . Dalam ruang yang sama, permukaan koordinat r = 1 dalam koordinat bola adalah permukaan bola satuan , yang melengkung. Formalisme koordinat lengkung memberikan gambaran umum dan terpadu dari sistem koordinat standar.
Terimakasih
NPM: 2013022013
Izin menjawab pertanyaan saudari Sri mengenai contoh sistem koordinat lengkung yang terkenal dalam ruang Euclidean tiga dimensi?
Contoh sistem koordinat lengkung yang terkenal dalam ruang Euclidean tiga dimensi ( R 3 ) adalah koordinat silinder dan bola . Permukaan koordinat Cartesian dalam ruang ini adalah bidang koordinat ; misalnya z = 0 mendefinisikan bidang x - y . Dalam ruang yang sama, permukaan koordinat r = 1 dalam koordinat bola adalah permukaan bola satuan , yang melengkung. Formalisme koordinat lengkung memberikan gambaran umum dan terpadu dari sistem koordinat standar.
Terimakasih
In reply to Sri Wahyu Lestari 2013022031
Re: Ayo Diskusi: Sistem Koordinat Bola
by Hana Lia 2013022027 -
Nama: Hana Lia
NPM: 2013022027
Izin menjawab pertanyaan dari saudari Sri Wahyu Lestari,
koordinat lengkung adalah sistem koordinat untuk ruang Euclidean di mana garis koordinat dapat melengkung. Koordinat ini dapat diturunkan dari himpunan koordinat Cartesius dengan menggunakan transformasi yang dapat dibalik secara lokal (peta satu-ke-satu) di setiap titik.
Contoh sistem koordinat lengkung yang terkenal dalam ruang Euclidean tiga dimensi ( R 3 ) adalah koordinat silinder dan bola . Permukaan koordinat Cartesian dalam ruang ini adalah bidang koordinat ; misalnya z = 0 mendefinisikan bidang x - y . Dalam ruang yang sama, permukaan koordinat r = 1 dalam koordinat bola adalah permukaan bola satuan , yang melengkung. Formalisme koordinat lengkung memberikan gambaran umum dan terpadu dari sistem koordinat standar.
Terima Kasih.
NPM: 2013022027
Izin menjawab pertanyaan dari saudari Sri Wahyu Lestari,
koordinat lengkung adalah sistem koordinat untuk ruang Euclidean di mana garis koordinat dapat melengkung. Koordinat ini dapat diturunkan dari himpunan koordinat Cartesius dengan menggunakan transformasi yang dapat dibalik secara lokal (peta satu-ke-satu) di setiap titik.
Contoh sistem koordinat lengkung yang terkenal dalam ruang Euclidean tiga dimensi ( R 3 ) adalah koordinat silinder dan bola . Permukaan koordinat Cartesian dalam ruang ini adalah bidang koordinat ; misalnya z = 0 mendefinisikan bidang x - y . Dalam ruang yang sama, permukaan koordinat r = 1 dalam koordinat bola adalah permukaan bola satuan , yang melengkung. Formalisme koordinat lengkung memberikan gambaran umum dan terpadu dari sistem koordinat standar.
Terima Kasih.
In reply to Sri Wahyu Lestari 2013022031
Re: Ayo Diskusi: Sistem Koordinat Bola
Nama: Yunita Safitri
Npm: 2013022039
Izin menjawab pertanyaan dari saudari Sri Wahyu Lestari,
Contoh sistem koordinat lengkung yang terkenal dalam ruang Euclidean tiga dimensi ( R 3 ) adalah koordinat silinder dan bola . Permukaan koordinat Cartesian dalam ruang ini adalah bidang koordinat ; misalnya z = 0 mendefinisikan bidang x - y . Dalam ruang yang sama, permukaan koordinat r = 1 dalam koordinat bola adalah permukaan bola satuan, yang melengkung. Formalisme koordinat lengkung memberikan gambaran umum dan terpadu dari sistem koordinat standar.
Koordinasi lengkung sering digunakan untuk menentukan lokasi atau distribusi besaran fisik yang mungkin, misalnya, skalar , vektor , atau tensor . Ekspresi matematika yang melibatkan kuantitas ini dalam kalkulus vektor dan analisis tensor (seperti gradien , divergensi , curl , dan Laplacian ) dapat diubah dari satu sistem koordinat ke sistem koordinat lainnya, sesuai dengan aturan transformasi untuk skalar, vektor, dan tensor. Ekspresi tersebut kemudian menjadi valid untuk setiap sistem koordinat lengkung.
Sistem koordinat lengkung mungkin lebih sederhana untuk digunakan daripada sistem koordinat Cartesian untuk beberapa aplikasi. Gerakan partikel di bawah pengaruh gaya pusat biasanya lebih mudah diselesaikan dalam koordinat bola daripada dalam koordinat Cartesian; ini benar untuk banyak masalah fisik dengan simetri bola yang didefinisikan dalam R 3 . Persamaan dengan kondisi batas yang mengikuti koordinat permukaan untuk sistem koordinat lengkung tertentu mungkin lebih mudah diselesaikan dalam sistem itu.Sementara orang mungkin menggambarkan gerakan partikel dalam kotak persegi panjang menggunakan koordinat Cartesian, gerakan dalam bola lebih mudah dengan koordinat bola. Koordinat bola adalah sistem koordinat lengkung yang paling umum dan digunakan dalam ilmu bumi , kartografi , mekanika kuantum , relativitas , dan teknik .
Sekian, terimakasih.
Npm: 2013022039
Izin menjawab pertanyaan dari saudari Sri Wahyu Lestari,
Contoh sistem koordinat lengkung yang terkenal dalam ruang Euclidean tiga dimensi ( R 3 ) adalah koordinat silinder dan bola . Permukaan koordinat Cartesian dalam ruang ini adalah bidang koordinat ; misalnya z = 0 mendefinisikan bidang x - y . Dalam ruang yang sama, permukaan koordinat r = 1 dalam koordinat bola adalah permukaan bola satuan, yang melengkung. Formalisme koordinat lengkung memberikan gambaran umum dan terpadu dari sistem koordinat standar.
Koordinasi lengkung sering digunakan untuk menentukan lokasi atau distribusi besaran fisik yang mungkin, misalnya, skalar , vektor , atau tensor . Ekspresi matematika yang melibatkan kuantitas ini dalam kalkulus vektor dan analisis tensor (seperti gradien , divergensi , curl , dan Laplacian ) dapat diubah dari satu sistem koordinat ke sistem koordinat lainnya, sesuai dengan aturan transformasi untuk skalar, vektor, dan tensor. Ekspresi tersebut kemudian menjadi valid untuk setiap sistem koordinat lengkung.
Sistem koordinat lengkung mungkin lebih sederhana untuk digunakan daripada sistem koordinat Cartesian untuk beberapa aplikasi. Gerakan partikel di bawah pengaruh gaya pusat biasanya lebih mudah diselesaikan dalam koordinat bola daripada dalam koordinat Cartesian; ini benar untuk banyak masalah fisik dengan simetri bola yang didefinisikan dalam R 3 . Persamaan dengan kondisi batas yang mengikuti koordinat permukaan untuk sistem koordinat lengkung tertentu mungkin lebih mudah diselesaikan dalam sistem itu.Sementara orang mungkin menggambarkan gerakan partikel dalam kotak persegi panjang menggunakan koordinat Cartesian, gerakan dalam bola lebih mudah dengan koordinat bola. Koordinat bola adalah sistem koordinat lengkung yang paling umum dan digunakan dalam ilmu bumi , kartografi , mekanika kuantum , relativitas , dan teknik .
Sekian, terimakasih.
In reply to Sri Wahyu Lestari 2013022031
Re: Ayo Diskusi: Sistem Koordinat Bola
by Putri Permata Sari -
Nama : Putri Permata Sari
Npm : 2013022029
Izin menjawab
Contoh sistem koordinat lengkung yang terkenal dalam ruang Euclidean tiga dimensi ( R 3 ) adalah koordinat silinder dan bola . Permukaan koordinat Cartesian dalam ruang ini adalah bidang koordinat ; misalnya z = 0 mendefinisikan bidang x - y . Dalam ruang yang sama, permukaan koordinat r = 1 dalam koordinat bola adalah permukaan bola satuan , yang melengkung. Formalisme koordinat lengkung memberikan gambaran umum dan terpadu dari sistem koordinat standar.
Terima kasih
Npm : 2013022029
Izin menjawab
Contoh sistem koordinat lengkung yang terkenal dalam ruang Euclidean tiga dimensi ( R 3 ) adalah koordinat silinder dan bola . Permukaan koordinat Cartesian dalam ruang ini adalah bidang koordinat ; misalnya z = 0 mendefinisikan bidang x - y . Dalam ruang yang sama, permukaan koordinat r = 1 dalam koordinat bola adalah permukaan bola satuan , yang melengkung. Formalisme koordinat lengkung memberikan gambaran umum dan terpadu dari sistem koordinat standar.
Terima kasih
Nama : Nada Nadidah
NPM : 2013022035
Izin menjawab,
Sistem koordinat 3d dalam ruang tiga dimensi, sistem koordinat Cartesian didasarkan pada tiga sumbu koordinat yang saling tegak lurus: sumbu x, sumbu y, dan sumbu z, seperti diilustrasikan di bawah ini. Ketiga sumbu tersebut berpotongan di titik yang disebut titik asal.
Contoh sistem koordinat lengkung yang terkenal dalam ruang Euclidean (R3) tiga dimensi adalah koordinat silinder dan bola. Permukaan koordinat Cartesian dalam ruang ini adalah bidang koordinat; misalnya z = 0 mendefinisikan bidang xy.
Terimakasih
NPM : 2013022035
Izin menjawab,
Sistem koordinat 3d dalam ruang tiga dimensi, sistem koordinat Cartesian didasarkan pada tiga sumbu koordinat yang saling tegak lurus: sumbu x, sumbu y, dan sumbu z, seperti diilustrasikan di bawah ini. Ketiga sumbu tersebut berpotongan di titik yang disebut titik asal.
Contoh sistem koordinat lengkung yang terkenal dalam ruang Euclidean (R3) tiga dimensi adalah koordinat silinder dan bola. Permukaan koordinat Cartesian dalam ruang ini adalah bidang koordinat; misalnya z = 0 mendefinisikan bidang xy.
Terimakasih
Nama: Gita Putri Rahmawati
NPM: 2013022009
Izin bertanya,
Berdasarkan pemaparan materi pada video ketiga, mengapa P (rho) pada koordinat bola selalu bernilai positif?
Terimakasih
NPM: 2013022009
Izin bertanya,
Berdasarkan pemaparan materi pada video ketiga, mengapa P (rho) pada koordinat bola selalu bernilai positif?
Terimakasih
In reply to Gita Putri Rahmawati 2013022009
Re: Ayo Diskusi: Sistem Koordinat Bola
Nama : Dea Citra Kharisma
NPM : 2013022003
Izin menjawab pertanyaan dari saudari Gita,
P (rho) pada koordinat bola adalah jarak dari asal ke titik, dan rho akan selalu lebih besar dari atau sama dengan nol. Oleh karena itu, rho pada koordinat bola selalu bernilai positif.
Mohon maaf apabila terdapat kekeliruan
Terimakasih.
NPM : 2013022003
Izin menjawab pertanyaan dari saudari Gita,
P (rho) pada koordinat bola adalah jarak dari asal ke titik, dan rho akan selalu lebih besar dari atau sama dengan nol. Oleh karena itu, rho pada koordinat bola selalu bernilai positif.
Mohon maaf apabila terdapat kekeliruan
Terimakasih.
In reply to Gita Putri Rahmawati 2013022009
Re: Ayo Diskusi: Sistem Koordinat Bola
Nama: Sri Wahyu Lestari
Npm: 2013022031
Izin menjawab pertanyaan dari Gita
Karena Koordinat bola ( r , , ) yang sering digunakan dalam matematika : jarak radial r , sudut azimut , dan sudut kutub . Arti dari dan telah ditukar dibandingkan dengan konvensi fisika. Seperti dalam fisika, ( rho ) sering digunakan sebagai pengganti r , untuk menghindari kebingungan dengan nilai r dalam koordinat kutub silinder dan 2D.
Terimakasih
Npm: 2013022031
Izin menjawab pertanyaan dari Gita
Karena Koordinat bola ( r , , ) yang sering digunakan dalam matematika : jarak radial r , sudut azimut , dan sudut kutub . Arti dari dan telah ditukar dibandingkan dengan konvensi fisika. Seperti dalam fisika, ( rho ) sering digunakan sebagai pengganti r , untuk menghindari kebingungan dengan nilai r dalam koordinat kutub silinder dan 2D.
Terimakasih
Nama : Annisa Qurottul Aini
NPM : 2013022043
Izin bertanya,
Bagaimana persamaan komponen variabel koordinat cartesian ke koordinat bola dan persamaan komponen variabel koordinat bola ke koordinat cartesian?
Terima kasih.
NPM : 2013022043
Izin bertanya,
Bagaimana persamaan komponen variabel koordinat cartesian ke koordinat bola dan persamaan komponen variabel koordinat bola ke koordinat cartesian?
Terima kasih.
In reply to Annisa Qurottul Aini 2013022043
Re: Ayo Diskusi: Sistem Koordinat Bola
Nama: Yunita Safitri
NPM: 2013022039
izin menjawab pertanyaan dari saudari Annisa,

Nama : Selia Febriyanti
NPM : 2013022015
Izin bertanya,
Apakah jawabannya akan sama ketika menggunakan koordinat silinder dan koordinat bola untuk masalah yang sama? Apa perbedaan antara sistem koordinat silinder dan sistem koordinat bola? Kapan sebaiknya menggunakan koordinat bola dan kapan koordinat silinder untuk berintegrasi?
Terimakasih
NPM : 2013022015
Izin bertanya,
Apakah jawabannya akan sama ketika menggunakan koordinat silinder dan koordinat bola untuk masalah yang sama? Apa perbedaan antara sistem koordinat silinder dan sistem koordinat bola? Kapan sebaiknya menggunakan koordinat bola dan kapan koordinat silinder untuk berintegrasi?
Terimakasih
In reply to Selia Febriyanti 83038544
Re: Ayo Diskusi: Sistem Koordinat Bola
Nama: Yunita Safitri
NPM: 2013022039
Izin menjawab pertanyaan dari saudari Selia,
Apakah jawabannya akan sama ketika menggunakan koordinat silinder dan koordinat bola untuk masalah yang sama?
Jika koordinat-invarian yang dapat dinyatakan murni dalam bentuk kuatitas itu sendiri daripada koordinat individu, maka jawabannya juga akan sama.
Apa perbedaan antara sistem koordinat silinder dan sistem koordinat bola?
perbedaan kedua sistem tersebut dijelaskan dalam diagram berikut:
NPM: 2013022039
Izin menjawab pertanyaan dari saudari Selia,
Apakah jawabannya akan sama ketika menggunakan koordinat silinder dan koordinat bola untuk masalah yang sama?
Jika koordinat-invarian yang dapat dinyatakan murni dalam bentuk kuatitas itu sendiri daripada koordinat individu, maka jawabannya juga akan sama.
Apa perbedaan antara sistem koordinat silinder dan sistem koordinat bola?
perbedaan kedua sistem tersebut dijelaskan dalam diagram berikut:
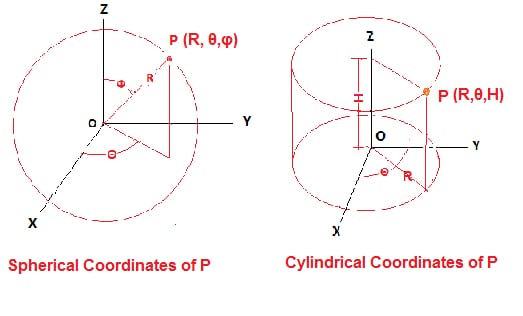
Perbedaan utama adalah bahwa sumbu z dan koordinatnya dipertahankan seperti aslinya dalam koordinat Cartesian untuk koordinat silinder dan pengenalan sudut azimut (sudut menjauh dari sumbu z) hanya untuk koordinat bola.
Kapan sebaiknya menggunakan koordinat bola dan kapan koordinat silinder untuk berintegrasi?
Umumnya lebih berkaitan dengan wilayah integrasi daripada fungsi. Jadi semakin baik untuk memvisualisasikan, membuat sketsa wilayah, yang akan membantu menemukan sistem parameterisasi / koordinat terbaik.
Koordinat bola sedikit lebih terspesialisasi. Koordinat silinder sedikit lebih fleksibel. Setiap masalah yang dapat diselesaikan dalam koordinat bola dapat diselesaikan dalam bentuk silinder, tetapi tidak harus sebaliknya. Jika ragu, gunakan silinder.
sekian, terimakasih.
nama : zulia natasys shofi
npm : 2053022001
izin bertanya
dijelaskan didalam video Ahli geografi dan navigasi menggunakan sistem koordinat yang sangat mendekati koordinat bola, yang disebut sistem tongitude dan latitude. apa yang dimaksud dengan sistem tongitude dan latitude dan apa kaitannya dengan koordinat bola tersebut
sekian terimakasih
npm : 2053022001
izin bertanya
dijelaskan didalam video Ahli geografi dan navigasi menggunakan sistem koordinat yang sangat mendekati koordinat bola, yang disebut sistem tongitude dan latitude. apa yang dimaksud dengan sistem tongitude dan latitude dan apa kaitannya dengan koordinat bola tersebut
sekian terimakasih
In reply to Zulia Natasya Sofi
Re: Ayo Diskusi: Sistem Koordinat Bola
Nama: Sri Wahu Lestari
NPM: 2013022031
Izin menjawa pertanyaan zulia
Sistem Longitude adalah garis lintang . Angka dari sudut bundar bumi horisontal.
Sedangkan Latitude adalah garis yang horisontal / mendatar. Titik 0 adalah sudut ekuator, tanda + menunjukan arah ke atas menuju kutub utara, sedangkan tanda minus di koordinat Latitude menuju ke kutub selatan.
Terimakasih
NPM: 2013022031
Izin menjawa pertanyaan zulia
Sistem Longitude adalah garis lintang . Angka dari sudut bundar bumi horisontal.
Sedangkan Latitude adalah garis yang horisontal / mendatar. Titik 0 adalah sudut ekuator, tanda + menunjukan arah ke atas menuju kutub utara, sedangkan tanda minus di koordinat Latitude menuju ke kutub selatan.
Terimakasih
In reply to Zulia Natasya Sofi
Re: Ayo Diskusi: Sistem Koordinat Bola
Nama: Ayu Iin Hidayah
NPM: 2013022017
Izin menjawab pertanyaan dari Zulia
Sistem Logitude itu artinya lintang, sedangkan latitude itu berarti bujur. Jadi Angka Latitude dan Longitude ini pada dasarnya adalah angka dalam sistem koordinat geografis. Dimana lintang dan bujur berkaitan erat dengan bola, maka sistem longitude dan latitude juga berkaitan dengan koordinat bola.
Sekian jawaban dari saya, mohon maaf apabila terdapat kekeliruan,
Terimakasih
NPM: 2013022017
Izin menjawab pertanyaan dari Zulia
Sistem Logitude itu artinya lintang, sedangkan latitude itu berarti bujur. Jadi Angka Latitude dan Longitude ini pada dasarnya adalah angka dalam sistem koordinat geografis. Dimana lintang dan bujur berkaitan erat dengan bola, maka sistem longitude dan latitude juga berkaitan dengan koordinat bola.
Sekian jawaban dari saya, mohon maaf apabila terdapat kekeliruan,
Terimakasih
Nama : Nada Nadidah
NPM : 2013022035
Izin bertanya,
Apa sistem koordinat yang digunakan untuk menggambarkan jalur lengkung?
Terimakasih
NPM : 2013022035
Izin bertanya,
Apa sistem koordinat yang digunakan untuk menggambarkan jalur lengkung?
Terimakasih
Nama : Galuh Wulan Safitri
NPM : 2013022007
Izin menjawab pertanyaan dari Nada,
Dalam sistem koordinat lengkung, jalur ini dapat dilengkungkan. Dua jenis koordinat lengkung adalah koordinat silinder dan bola. Sistem koordinat silinder adalah tiga dimensi sistem koordinat yang menentukan titik posisi dengan jarak dari sumbu referensi yang dipilih, arah dari sumbu relatif terhadap arah referensi yang dipilih, dan jarak dari pesawat referensi yang dipilih tegak lurus dengan sumbu. Jarak terakhir diberikan sebagai angka positif atau negatif tergantung pada sisi bidang referensi mana yang menghadap titik.
Sistem koordinat bola adalah sistem koordinat untuk ruang tiga dimensi di mana posisi suatu titik ditentukan oleh tiga angka : jarak radial titik tersebut dari titik asal tetap, sudut kutubnya diukur dari arah zenit tetap , dan yang sudut azimut nya proyeksi ortogonal pada bidang referensi yang melewati asal dan ortogonal untuk zenit, diukur dari arah referensi tetap di pesawat itu. Ini dapat dilihat sebagai versi tiga dimensi dari sistem koordinat kutub .
Mohon maaf bila terdapat kesalahan dalam menjawab pertanyaan,
Terimakasih.
NPM : 2013022007
Izin menjawab pertanyaan dari Nada,
Dalam sistem koordinat lengkung, jalur ini dapat dilengkungkan. Dua jenis koordinat lengkung adalah koordinat silinder dan bola. Sistem koordinat silinder adalah tiga dimensi sistem koordinat yang menentukan titik posisi dengan jarak dari sumbu referensi yang dipilih, arah dari sumbu relatif terhadap arah referensi yang dipilih, dan jarak dari pesawat referensi yang dipilih tegak lurus dengan sumbu. Jarak terakhir diberikan sebagai angka positif atau negatif tergantung pada sisi bidang referensi mana yang menghadap titik.
Sistem koordinat bola adalah sistem koordinat untuk ruang tiga dimensi di mana posisi suatu titik ditentukan oleh tiga angka : jarak radial titik tersebut dari titik asal tetap, sudut kutubnya diukur dari arah zenit tetap , dan yang sudut azimut nya proyeksi ortogonal pada bidang referensi yang melewati asal dan ortogonal untuk zenit, diukur dari arah referensi tetap di pesawat itu. Ini dapat dilihat sebagai versi tiga dimensi dari sistem koordinat kutub .
Mohon maaf bila terdapat kesalahan dalam menjawab pertanyaan,
Terimakasih.
