Silakan Anda diskusikan materi Osilator Harmonik pada 2-3 Dimensi yang ada pada buku Analytical Mechanics (Fowles & Cassiday) atau sumber lainnya pada forum ini. Jika ada hal yang perlu ditanyakan juga silakan disampaikan pada forum ini.
Ayo Diskusi: Osilator Harmonik pada 2-3 Dimensi
Re: Ayo Diskusi: Osilator Harmonik pada 2-3 Dimensi
NPM : 2013022008
Izin bertanya,
Pada materi ini terdapat osilator harmonik 2-3 dimensi isotropik dan tidak isotropik. Bagaimana cara membedakan benda yang bergerak osilator harmonik isotropik dan tidak isotropik tersebut?
Terima kasih
Re: Ayo Diskusi: Osilator Harmonik pada 2-3 Dimensi
NPM : 2013022054
Izin menjawab, cara membedakannya adalah ditinjau dari arah pergesarannya. Jika gaya pemulihannya tak bergantung pada arah pergeseran maka benda bergerak isotropik. Jika gaya pemulihannya bergantung pada arah pergeseran, maka osilatornya disebut tidak isotropik.
Terima kasih
Re: Ayo Diskusi: Osilator Harmonik pada 2-3 Dimensi
NPM : 2013022002
Izin bertanya,
Pada bahasan osilator harmonik pada 2-3 dimensi ini, yang ingin saya tanyakan adalah apa yang terjadi jika besaran komponen gaya pemulih bergantung pada arah perpindahan? Deskripsikan.
Terima kasih
Re: Ayo Diskusi: Osilator Harmonik pada 2-3 Dimensi
NPM: 2013022050
Izin menjawab,
Jika besaran komponen gaya pemulihan bergantung pada arah perpindahan, maka osilatornya tidak isotropik
Terima Kasih.
Re: Ayo Diskusi: Osilator Harmonik pada 2-3 Dimensi
NPM : 2013022062
Izin bertanya,
Berdasarkan materi mengenai osilator harmonik ini yang ingin saya tanyakan adalah Mengapa energi pada keadaan dasar osilator harmonik sederhana kuantum tidak nol? Berikan penjelasannya
Terimakasih
Re: Ayo Diskusi: Osilator Harmonik pada 2-3 Dimensi
Npm : 2013022006
Izin menjawab,
Hal itu dikarenakan hasil dari prinsip Heisenberg. Jika momentum tidak dapat didefinisikan dengan baik, itu tidak bisa menjadi nol, sehingga partikel memiliki energi yang tidak nol. Sebagian besar waktu Anda dapat menggeser skala energi dengan jumlah yang tetap dan menempatkan keadaan dasar pada energi nol. Tapi ini tidak selalu mungkin (mis. Relativitas umum).
Terimakasih.
Re: Ayo Diskusi: Osilator Harmonik pada 2-3 Dimensi
Npm: 2013022056
Izin bertanya,
Bagaimana penerapan osilator harmonik dalam kehidupan sehari-hari?
Terimakasih
Re: Ayo Diskusi: Osilator Harmonik pada 2-3 Dimensi
NPM :2013022058
Izin menjawab,
Aplikasi dari osilator harmonik pada kehidupan sehari-hari antara lain gerak harmonik pada bandul gerak harmonik pada pegas, kejut (shock absorber) pada mobil jam mekanik dan garpu tala.
Terimakasih
Re: Ayo Diskusi: Osilator Harmonik pada 2-3 Dimensi
NPM : 2013022038
Izin menambahkan,
Fenomena osilasi tidak hanya terjadi pada dunia fisika atau tidak hanya didominasi oleh contoh-contoh di bidang fisika, namun nyatanya fenomena ini adalah fenomena alamiah ilmiah yang terjadi didalam kehidupan manusia sesungguhnya. Banyak contoh nyata dalam kehidupan manusia yang berkaitan erat dengan fenomena ini seperti bandul yang otomatis terus berputar, ayunan, kipas angin bergerak kekekiri dan kekanan, pergantian siang dan malam, gerakan pegas, winter dan summer, detak jantung manusia, bekerja dan istirahat, dan masih banyak lagi lainnya.
Terimakasih
Re: Ayo Diskusi: Osilator Harmonik pada 2-3 Dimensi
Npm : 2013022048
Izin Bertanya,
Osilator harmonik juga dapat diartikan sebagai suatu sistem yang bergetar dimana gaya pemulih berbanding lurus dengan negatif simpangannya. Mengapa Pernyataan tersebut Selalu Menghasilkan Negatif Simpangannya?
Terima Kasih.
Re: Ayo Diskusi: Osilator Harmonik pada 2-3 Dimensi
NPM: 2013022016
Izin menjawab,
Gaya pemulih merupakan gaya yang bekerja dalam arah mengembalikan massa benda ke posisi kesetimbangannya. Tanda negatif pada simpangan untuk menunjukkan bahwa arah gaya pemulih selalu berlawanan dengan arah gerak pegas. Jika sebuah pegas diberi gangguan sehingga pegas meregang (berarti pegas ditarik).
Terimakasih.
Re: Ayo Diskusi: Osilator Harmonik pada 2-3 Dimensi
NPM: 2013022004
Izin menjawab,
Tanda (-) negatif menunjukkan bahwa arah gaya pemulih yang senantiasa menuju ke titik kesetimbangan selalu berlawanan dengan arah gaya penyebabnya atau arah simpangannya.
Terima kasih
Re: Ayo Diskusi: Osilator Harmonik pada 2-3 Dimensi
NPM : 2013022014
Izin bertanya,
Bagaimana tinjauan osilator harmonik dalam mekanika kuantum?
Terimakasih
Re: Ayo Diskusi: Osilator Harmonik pada 2-3 Dimensi
NPM : 2013022030
Izin menjawab,
Dalam mekanika kuantum, fungsi gelombang dari osilator harmonik diperoleh dengan memecahkan persamaan SchrÖdinger dengan potensial V(x) berbentuk
V(x) = 1/2mω2x2
Oleh karena V(x) tidak bergantung waktu, maka dapat menggunakan persamaan SchrÖdinger tak bergantung waktu bentuk satu dimensi.
Terima KasihNpm : 2013022010
izin bertanya,
saat membentangkan pegas terlalu panjang akan mengakibatkan getaran berhenti, pada osilator harmonik sederhana. mengapa demikian?
terimakasih
Re: Ayo Diskusi: Osilator Harmonik pada 2-3 Dimensi
NPM: 2013022004
Izin menjawab,
Jika kita membentangkan pegas terlalu panjang, bisa-bisa pegas tersebut akan berhenti bergetar karena sudah melewati titik elastisitasnya dan juga hukum Hooke tidak akan berlaku untuk kasus yang demikian. Tetapi praktisnya, potensial dapat didekati dengan fungsi parabola, di dalam titik tetangga dari titik minimum.
Terima kasih
Re: Ayo Diskusi: Osilator Harmonik pada 2-3 Dimensi
Nama : Nadiyah Safitri
NPM : 2013022046
Izin menambahkan,
Jika kita membentangkan pegas terlalu panjang, bisa-bisa pegas tersebut akan berhenti bergetar karena sudah melewati titik elastisitasnya dan juga hukum Hooke tidak akan berlaku untuk kasus yang demikian. Tetapi praktisnya, potensial dapat didekati dengan fungsi parabola, di dalam titik tetangga dari titik minimum (Gambar 1.1), Formalnya, jika kita mengekspansi V(χ) ke dalam deret Taylor di sekitar titik minimum, maka
V(χ) = V (χ0) +V’ (χ0)( χ- χ0) + V” (χ0)( χ- χ0)2 +……..
Bagilah dengan V (χ0)
[Kita juga bisa menambah konstanta sembarang pada V(χ) selama tidak mengubah gaya], misalkan ![]() yang menggambarkan gerak oslilasi selaras sederhana (di sekitar titik x0),
dengan konstanta pegas efetif K=V”(χ0). Inilah kenapa oslilator
selaras sederhana menjadi sangat penting dalam mekanika kuantum, secara kasat
mata gerak osilator adalah selaras sederhana selama nilai amplitudonya kecil.
yang menggambarkan gerak oslilasi selaras sederhana (di sekitar titik x0),
dengan konstanta pegas efetif K=V”(χ0). Inilah kenapa oslilator
selaras sederhana menjadi sangat penting dalam mekanika kuantum, secara kasat
mata gerak osilator adalah selaras sederhana selama nilai amplitudonya kecil.
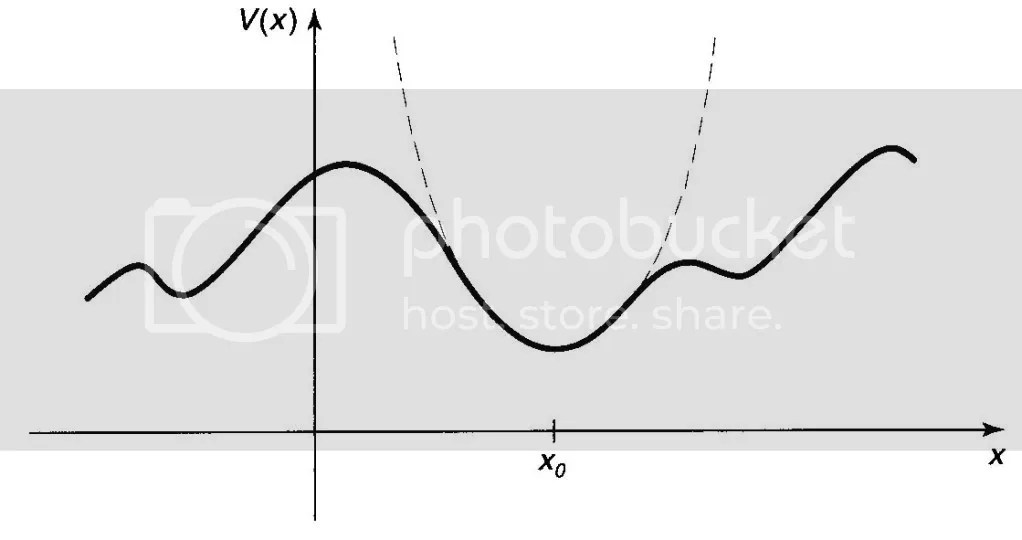
Gambar 1.1 : Pendekatan parabolik (kurva putus-putus) pada potensial sembarang, di antara titik minimum.
Terima kasih
